Leapfrog and forward Euler numerical integration.

In this post I’m showing how to program a Leap-Frog integrator. Its performance of it is compared to the Forward-Euler integration method and an analytical solution. The methods are for solving ordinary differential equations. A MATLAB program shows how the methods can be implemented.

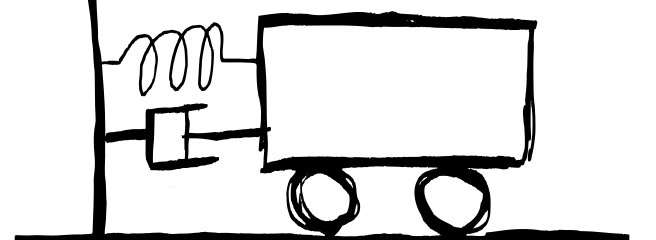
For the testing, a very simple mechanical system is considered. It consists of a body with mass m = 2, a spring with stiffness k = 4 and a damper with damping c = 1.

The body acceleration is calculated at a given time step by evaluating the equation of motion (Newton’s second low) given the instantaneous position and velocity

\ddot{x}_{i} = a(x, \dot{x})

Based on that acceleration the velocity can be calculated half a step in advance

\dot{x}_{i+0.5} = \dot{x}_{i-0.5} + \ddot{x}_{i}\cdot h

Where h is the step size often measured in seconds. Now the position to the next full time step can be calculated

x_{i+1} = x_{i} + \dot{x}_{i+0.5}\cdot h

But we also need to calculate the velocity at the next full time step in order to be able to calculate the next acceleration. The next velocity can be estimated by this first order finite difference (it is only a true finite difference when s =1)

\dot{x}_{i+1} = \dot{x}{i+0.5}+(\dot{x}_{i+0.5}-\dot{x}_{i})\cdot s

where s is a stability constant which might take any value in the range from -0.25 to 1.

And now to the programming

The test case is a simple one-dimensional system consisting of a mass, spring and damper with the properties:

m = 2;
k = 40;
c = 1;

Define a function for calculation of acceleration given the position q and velocity \dot{q}. The resulting force on the mass is simply F = -k\cdot q-c\cdot \dot{q}, then, the acceleration can be calculated using Newtons second law.

function ddq = Acceleration(q, dq)
ddq = (-kq -cdq)/m;
end

The solution to the differential equation will be calculated to the discrete time given here:

t = linspace(0, 3, 40);
% the time step size
h = t(2)-t(1);
% Vectors for the results are prealocated here
euler = struct(... 
    'x',zeros(size(t)),...
    'dx',zeros(size(t)),...
    'ddx',zeros(size(t)));
lf = struct(...
    'x',zeros(size(t)),...
    'dx',zeros(size(t)),...
    'ddx',zeros(size(t)));

To find a specific solution one must specify some boundary conditions. In this case the initial position and velocity of the particle is given.

x0 = 1;
dx0 = 0.5;
euler.x(1) = x0;
lf.x(1) = x0;
euler.dx(1) = dx0;
lf.dx(1) = dx0;

% Aclculate the accelerations given the initail 
% conditions
euler.ddx(1) = Acceleration(euler.x(1), euler.dx(1));
lf.ddx(1) = Acceleration(lf.x(1), lf.dx(1));

% For the Leap-Forg the velocity is calculated half a
% time-step in advance. This half-step must be 
% initailized as well.
lf_dx = lf.dx(1) + lf.ddx(1) * 0.5 * h;

The stability factor is artificial damping. Funny enough, the more damping you put into the model, the more stability is required, hence, a lower stability factor should be selected. The value can be any number in the range from 1 to -0.25. Choosing low numbers compromise the frequency response. Choosing stability = -0.25 is almost equivalent to the average approach.

stability = 0.62;

for i=1:length(t)-1
    % Forward euler integration
    euler.dx(i+1) = euler.dx(i) + euler.ddx(i)*h;
    euler.x(i+1) = euler.x(i) + euler.dx(i)*h;
    euler.ddx(i+1) = Acceleration(...
                    euler.x(i+1), euler.dx(i+1));
    
    % Leap-Frog integration
    lf.x(i+1) = lf.x(i) + lf_dx*h;
    
    % Velocity at full step
    lf.dx(i+1) = lf_dx + (lf_dx - lf.dx(i)) * stability;

    lf.ddx(i+1) = Acceleration(lf.x(i+1), lf.dx(i+1));
    lf_dx = lf_dx + lf.ddx(i+1)*h;
end

% Analytic solution
omega_n = sqrt(k/m);
xi = c / (2*sqrt(k*m));
omega_d = omega_n*sqrt(1-xi^2);
x = exp(-xi*omega_n*t) .* (x0*cos(omega_d*t) + ...
       (dx0 + xi*omega_n*x0)./omega_d*sin(omega_d*t));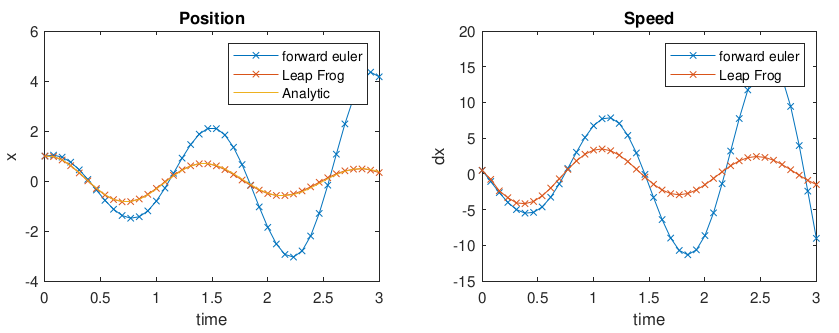

Leapfrog is much better than Forward-Euler for this simple mechanical system, at least based on the plots above. It is almost identical to the analytic solution – but in more complicated systems, the Leap-Frog is not as convincing.